Trắc Nghiệm Toán 12 Cánh Diều Ôn Tập Cuối Chương 4 là bộ đề ôn tập tổng hợp kiến thức môn Toán lớp 12, bám sát nội dung sách giáo khoa Cánh Diều. Đề do thầy Lê Minh Đức – giáo viên môn Toán tại Trường THPT Nguyễn Khuyến biên soạn năm học 2024–2025. Đây là bài học tổng kết quan trọng của “Chương IV: Nguyên hàm. Tích phân”, xoay quanh toàn bộ kiến thức về định nghĩa, tính chất, các phương pháp tìm nguyên hàm, tính tích phân và ứng dụng hình học để tính diện tích, thể tích. Bộ câu hỏi trắc nghiệmToán 12 Cánh diều này là tài liệu quan trọng giúp học sinh hệ thống hóa kiến thức, chuẩn bị cho bài kiểm tra cuối học kỳ.
Hệ thống Trắc nghiệm môn Toán 12 trên nền tảng detracnghiem.edu.vn được thiết kế để giúp học sinh tổng hợp và củng cố kiến thức một cách hiệu quả. Với kho câu hỏi đa dạng, bao quát toàn bộ chương 4 và được phân loại theo mức độ từ nhận biết đến vận dụng cao, học sinh có thể thực hành không giới hạn để kiểm tra lại kiến thức. Mỗi câu hỏi đều đi kèm đáp án và lời giải chi tiết, giúp các em không chỉ biết đáp án đúng mà còn hiểu rõ bản chất của từng phương pháp tính toán. Biểu đồ phân tích tiến độ học tập cá nhân giúp học sinh tự đánh giá mức độ hiểu bài, từ đó có định hướng rõ ràng hơn cho việc ôn tập. Đây là phương pháp học tập hiện đại, giúp học sinh tự tin chinh phục các bài Trắc nghiệm ôn thi 12.
Trắc Nghiệm Toán 12 Cánh Diều Có Đáp Án
Ôn tập cuối Chương 4: Nguyên hàm – Tích phân
Câu 1: Cho hàm số $f(x) = 2x + e^x$. Nguyên hàm $F(x)$ của hàm số $f(x)$ trên $\mathbb{R}$ sao cho $F(0) = 2023$ là:
A. $x^2 + e^x + 2023$.
B. $x^2 + e^x + C$.
C. $x^2 + e^x + 2022$.
D. $x^2 + e^x$.
Câu 2: Biết $F(x) = x^3$ là một nguyên hàm của hàm số $f(x)$ trên $\mathbb{R}$. Giá trị của $\int_1^2 [f(x) + 2]dx$ bằng:
A. 23/4.
B. 7.
C. 9.
D. 15/4.
Câu 3: Biết $\int_1^2 f(x)dx = 2$. Khi đó, $\int_1^2 [f(x) + 2x]dx$ bằng:
A. 5.
B. 1.
C. 4.
D. 2.
Câu 4: Tìm nguyên hàm của hàm số $f(x) = 2x^3 – x^2 + 2$.
A. $\frac{1}{2}x^4 – \frac{1}{3}x^3 + 2x – 1$.
B. $\frac{1}{2}x^4 – \frac{1}{3}x^3 + 2x + C$.
C. $\frac{1}{2}x^4 – \frac{1}{2}x^3 + 2x + C$.
D. $\frac{1}{2}x^4 + \frac{1}{3}x^3 + 2x + C$.
Câu 5: Tìm nguyên hàm của hàm số $f(x) = (2x + \frac{1}{x})^2$.
A. $2x^2 + \frac{1}{x} + C$.
B. $\frac{4}{3}x^3 + 4x – \frac{1}{x} + C$.
C. $\frac{4}{3}x^3 – \frac{1}{x} + C$.
D. $\frac{4}{3}x^3 – \frac{1}{x} + 4x + C$.
Câu 6: Tìm nguyên hàm của hàm số $f(x) = 3 + 2\tan^2 x$.
A. $3x + 2\tan x + C$.
B. $3x + 2\tan x – 2x + C$.
C. $x + 2\tan x + C$.
D. $4x + 3\tan x + C$.
Câu 7: Tìm nguyên hàm của hàm số $f(x) = (1 – 3\cot^2 x)$.
A. $x + 3\cot x + C$.
B. $x – 3\cot x + C$.
C. $x + 3\cot x + 3x + C$.
D. $4x + 3\cot x + C$.
Câu 8: Tìm nguyên hàm của hàm số $f(x) = \sin(2x + 1)$.
A. $-\frac{1}{2}\cos(2x + 1) + C$.
B. $-\cos(2x + 1) + C$.
C. $\frac{1}{2}\cos(2x + 1) + C$.
D. $-2\cos(2x + 1) + C$.
Câu 9: Tìm nguyên hàm của hàm số $f(x) = 2.6^{-x}$.
A. $2 \cdot 6^{-x} \cdot \ln 6 + C$.
B. $2 \cdot 6^{-x} / \ln 6 + C$.
C. $-2 \cdot 6^{-x} \cdot \ln 6 + C$.
D. $-2 \cdot 6^{-x} / \ln 6 + C$.
Câu 10: Cho hàm số $f(x) = x^3 + e^x$. Tìm nguyên hàm $F(x)$ của hàm số $f(x)$ trên $\mathbb{R}$ sao cho $F(0) = 2023$.
A. $\frac{x^4}{4} + e^x + 2023$.
B. $\frac{x^4}{4} + e^x + C$.
C. $\frac{x^4}{4} + e^x + 2022$.
D. $\frac{x^4}{4} + e^x + 2021$.
Câu 11: Cho hàm số $g(x) = \frac{1}{x}$ ($x > 0$). Tìm nguyên hàm $G(x)$ của hàm số $g(x)$ trên khoảng $(0; +\infty)$ sao cho $G(1) = 2023$.
A. $\ln x + 2023$.
B. $\ln|x| + 2023$.
C. $\ln x + C$.
D. $\ln x + 2022$.
Câu 12: Tính $\int_{-1}^1 (x + 2)^3 dx$.
A. 16.
B. 18.
C. 10.
D. 8.
Câu 13: Tính $\int_1^2 \frac{1}{x^2} dx$.
A. 1/2.
B. 1.
C. 2.
D. 3/2.
Câu 14: Tính $\int_1^4 \frac{1}{x\sqrt{x}} dx$.
A. 1.
B. 2.
C. 1/2.
D. 3/2.
Câu 15: Tính $\int_0^1 2^{3x+2} dx$.
A. $\frac{32}{3 \ln 2}$.
B. $\frac{32}{\ln 2}$.
C. $\frac{32}{ \ln 8}$.
D. $\frac{28}{3 \ln 2}$.
Câu 16: Tính $\int_0^2 2^{3x+2} dx$.
A. $\frac{1020}{3 \ln 2}$.
B. $\frac{1024}{3 \ln 2}$.
C. $\frac{1024}{\ln 2}$.
D. $\frac{1020}{3 \ln 2}$.
Câu 17: Tính $\int_{-1}^1 \frac{1}{7^x} dx$.
A. $\frac{48}{7 \ln 7}$.
B. $\frac{24}{\ln 7}$.
C. $\frac{48}{\ln 7}$.
D. $\frac{48}{\ln 7}$.
Câu 18: Một khinh khí cầu bay với độ cao $h(t)$ (trong đó $t$ tính bằng phút) và vận tốc $v(t) = -0,12t^2 + 1,2t$ (m/phút). Tại thời điểm xuất phát ($t=0$), khinh khí cầu ở độ cao 520 m. Viết công thức xác định hàm số $h(t)$ ($0 \le t \le 29$).
A. $h(t) = -0,04t^3 + 0,6t^2$.
B. $h(t) = -0,04t^3 + 0,6t^2 + 520$.
C. $h(t) = -0,12t^3 + 1,2t^2 + 520$.
D. $h(t) = -0,04t^3 + 0,6t^2 + 500$.
Câu 19: Một khinh khí cầu bay với độ cao $h(t)$ (trong đó $t$ tính bằng phút) và vận tốc $v(t) = -0,12t^2 + 1,2t$ (m/phút). Tại thời điểm xuất phát ($t=0$), khinh khí cầu ở độ cao 520 m. Khi khinh khí cầu ở độ cao 530 m thì đã bay bao nhiêu?
A. 15 phút.
B. 10 phút.
C. 20 phút.
D. 5 phút.
Câu 20: Một công trình xây dựng dự kiến hoàn thành trong 100 ngày. Số lượng công nhân được sử dụng tại thời điểm $t$ cho bởi hàm số $m(t) = 500 + 50t – t^2$. Hỏi khi nào thì 360 công nhân được sử dụng?
A. $t = 20$ hoặc $t = 30$.
B. $t = 10$ hoặc $t = 40$.
C. $t = 5$ hoặc $t = 45$.
D. $t = 15$ hoặc $t = 35$.
Câu 21: Một công trình xây dựng dự kiến hoàn thành trong 100 ngày. Số lượng công nhân được sử dụng tại thời điểm $t$ cho bởi hàm số $m(t) = 500 + 50t – t^2$. Hỏi khi nào số công nhân được sử dụng lớn nhất?
A. $t = 15$.
B. $t = 20$.
C. $t = 25$.
D. $t = 30$.
Câu 22: Gọi $M(t)$ là số ngày công được tính đến hết ngày thứ $t$. Tổng số ngày công để hoàn thành công trình xây dựng, biết $m'(t) = m(t)$ là 100 ngày.
A. 40000 ngày công.
B. 50000 ngày công.
C. 60000 ngày công.
D. 45000 ngày công.
Câu 23: Trong bài này, ta xét một tình huống giả định có một học sinh sau khi nghỉ đã mang virus cúm quay trở lại khuôn viên trường học bị lây bởi 1000 học sinh. Biết rằng tốc độ lây lan của virus cúm tỉ lệ thuận với số học sinh không bị nhiễm virus cúm theo hệ số $k=0$. Số học sinh bị nhiễm virus cúm sau 4 ngày là 52 học sinh. Xác định số học sinh bị nhiễm virus cúm sau 10 ngày.
A. 136 học sinh.
B. 140 học sinh.
C. 144 học sinh.
D. 148 học sinh.
Câu 24: Một chiếc xe ô tô chạy thử nghiệm trên một đường thẳng bắt đầu từ trạng thái đứng yên. Tốc độ của chiếc xe ô tô đó (tính bằng mét/giây) lần lượt ở giây 10, 20, 30, 40, 50 và 60 được ghi lại trong Bảng 1. Hãy tính (gần đúng) quãng đường mà xe ô tô đó đã đi được tính đến giây thứ 60.
A. 3200 mét.
B. 3800 mét.
C. 4000 mét.
D. 3500 mét.
Câu 25: Giả sử $A, B$ lần lượt là diện tích các hình được tô màu ở Hình 37. Tính diện tích $A$.
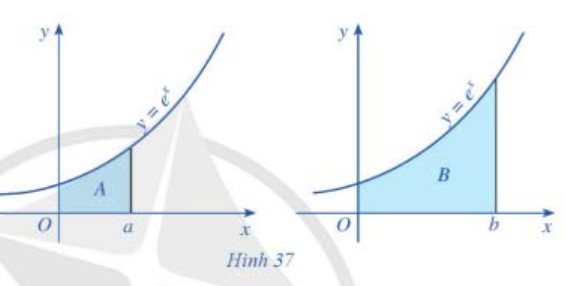
A. $A = 1/3$.
B. $A = 2/3$.
C. $A = 1$.
D. $A = 1/2$.
Câu 26: Giả sử $A, B$ lần lượt là diện tích các hình được tô màu ở Hình 37. Biết $B = 3A$. Biểu diễn $b$ theo $a$.

A. $b = a^3$.
B. $b = a^2$.
C. $b = a^{1/3}$.
D. $b = a^3$.
Câu 27: Hình 38 minh họa mặt cắt đứng của một bức tường cũ có dạng hình chữ nhật với một cổng ra vào có dạng hình parabol với các kích thước được cho như trong hình đó. Chi phí để sơn bức tường là 15.000 đồng/1 m$^2$. Tính tổng chi phí để sơn lại toàn bộ mặt ngoài của bức tường đó.
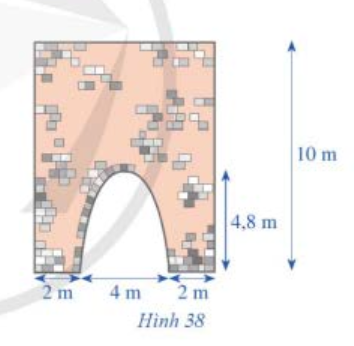
A. 1.100.000 đồng.
B. 1.500.000 đồng.
C. 1.800.000 đồng.
D. 1.200.000 đồng.
Câu 28: Cho khối tròn xoay Hình 39. Hình phẳng được giới hạn bởi các đường nào để khi quay quanh trục $Ox$ ta được khối tròn xoay như Hình 39?
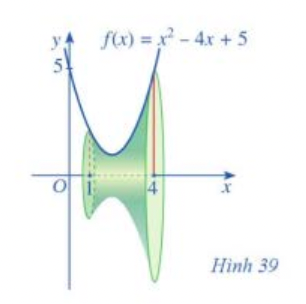
A. $y = x^2 – 4x + 5$, $y = 0$.
B. $y = x^2 – 4x + 5$, $x=0$.
C. $y = x^2 – 4x + 5$, $y=1$.
D. $y = x^2 – 4x + 5$, $y=-1$.
Câu 29: Cho khối tròn xoay Hình 39. Tính thể tích khối tròn xoay đó.

A. $\frac{8}{5}\pi$.
B. $\frac{16}{15}\pi$.
C. $\frac{2\sqrt{5}}{3}\pi$.
D. $\frac{32}{15}\pi$.
Câu 30: Cho hàm số $f(x) = ax^3 + bx^2 + cx + d$ ($a \ne 0$) để biểu diễn các số liệu ở Bảng 1 (Bài 10, trang 62). $D(30; 40)$. Tìm giá trị $a, b, c, d$ để hàm số này phù hợp với các điểm $O(0;0)$, $B(10;5)$, $C(20;21)$, $D(30;40)$, $E(40;62)$, $G(50;78)$, $K(60;83)$.
A. $a = 0,001$.
B. $b = -0,02$.
C. $c = 0,1$.
D. $d = 0$.


