Đề thi thử tốt nghiệp THPT năm 2025 môn Toán – Sở GD&ĐT Lâm Đồng là một trong những đề nổi bật thuộc chương trình Thi thử Toán THPT, nằm trong chuyên mục Ôn tập thi thử THPT, hướng đến hỗ trợ học sinh lớp 12 trong quá trình chuẩn bị cho kỳ thi tốt nghiệp cũng như các kỳ thi chuyển cấp quan trọng.
Đề thi được biên soạn bám sát cấu trúc của Bộ GD&ĐT, bao gồm đầy đủ các chuyên đề trọng tâm: hàm số, mũ – logarit, nguyên hàm – tích phân, hình học không gian, số phức, xác suất – thống kê và các bài toán vận dụng thực tiễn. Mức độ câu hỏi được phân hóa rõ ràng, giúp học sinh rèn luyện kỹ năng giải toán toàn diện từ nhận biết đến vận dụng cao.
Khám phá ngay đề thi tại Dethitracnghiem.vn để bắt đầu quá trình ôn tập hiệu quả cho kỳ thi THPT năm 2025 trong giai đoạn quan trọng này.
Đề thi thử tốt nghiệp THPT năm 2025 môn Toán sở GD&ĐT Lâm Đồng Có Đáp Án Chi Tiết
PHẦN I. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án
Câu 1. Thầy Lâm thống kê lại đường kính thân gỗ của một số cây xoan đào 6 năm tuổi được trồng ở sân trường thu được mẫu số liệu ghép nhóm sau:
 Khoảng biến thiên của mẫu số liệu ghép nhóm trên là
Khoảng biến thiên của mẫu số liệu ghép nhóm trên là
A. 15.
B. 6.
C. 30.
D. 25.
Câu 2. Trong không gian Oxyz, tọa độ tâm I của mặt cầu $(S): (x-1)^2 + y^2 + (z+2)^2 = 9$ là
A. I(1; 0; -2).
B. I(-1; 0; 2).
C. I(-1; 1; 2).
D. I(1; 1; -2).
Câu 3. Trong không gian Oxyz, cho hai điểm $M(-1; -1; 2)$ và $N(1; 3; 4)$. Đường thẳng MN có phương trình chính tắc là
A. $\frac{x+1}{1} = \frac{y+1}{2} = \frac{z-2}{1}$.
B. $\frac{x+1}{2} = \frac{y+3}{4} = \frac{z+4}{2}$.
C. $\frac{x-1}{2} = \frac{y-1}{4} = \frac{z+2}{2}$.
D. $\frac{x-1}{2} = \frac{y-1}{2} = \frac{z+2}{1}$.
Câu 4. Cho cấp số nhân $(u_n)$ với $u_1 = 3$ và công bội $q = 2$. Giá trị của $u_3$ bằng
A. 12.
B. 7.
C. 18.
D. 6.
Câu 5. Trong không gian Oxyz, cho mặt phẳng $(P): 2x – 3y + z – 5 = 0$. Vectơ nào sau đây là một vectơ pháp tuyến của mặt phẳng $(P)$?
A. $\vec{n}(2; -3; 5)$.
B. $\vec{n}(2; -3; 1)$.
C. $\vec{n}(2; 3; -1)$.
D. $\vec{n}(2; -3; -5)$.
Câu 6. Tập nghiệm của bất phương trình $2^x \le 3$ là
A. $[\log_2 3; +\infty)$.
B. $(-\infty; \log_2 3)$.
C. $(\log_2 3; +\infty)$.
D. $(-\infty; \log_2 3]$.
Câu 7. Nghiệm của phương trình $\log_3(2x – 1) = 2$ là
A. x = 5.
B. x = 3.
C. $x = \frac{7}{2}$.
D. $x = \frac{9}{2}$.
Câu 8. Nguyên hàm của hàm số $f(x) = x^3 + x$ là
A. $\frac{1}{4}x^4 + \frac{1}{2}x^2 + C$.
B. $x^4 + x^2 + C$.
C. $x^3 + x + C$.
D. $3x^2 + 1 + C$.
Câu 9. Biết $F(x)=x^3$ là một nguyên hàm của hàm số $f(x)$ trên $\mathbb{R}$. Giá trị của $\int_{1}^{2}[2+f(x)]dx$ bằng
A. $\frac{23}{4}$.
B. $\frac{15}{4}$.
C. 7.
D. 9.
Câu 10. Hàm số nào dưới đây có đồ thị như hình vẽ bên?
A. $y = x^3 – 3x + 1$.
B. $y = \frac{2x+1}{x+1}$.
C. $y = \frac{2x-1}{x-1}$.
D. $y = 2x + \frac{1}{x+1}$.
Câu 11. Một khối chóp có đường cao $h = 3a$ và diện tích đáy $B = a^2$. Thể tích khối chóp đó bằng
A. $a^3$.
B. $\frac{a^3}{2}$.
C. $3a^3$.
D. $\frac{3a^3}{2}$.
Câu 12. Cho hàm số $y = f(x)$ có bảng biến thiên như sau:
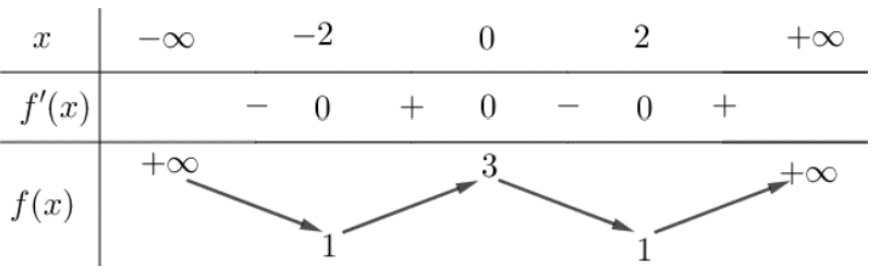
Giá trị cực đại của hàm số đã cho bằng
A. 2.
B. 3.
C. 1.
D. 0.
PHẦN II. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 1. Một ô tô đang di chuyển với vận tốc $21(m/s)$, khi còn cách trạm thu phí một đoạn thì người lái xe bắt đầu đạp phanh lần một, xe chuyển động thẳng chậm dần đều với vận tốc biến thiên theo thời gian được xác định bởi quy luật $v_1(t)=-6t+21(m/s)$, trong đó thời gian $t$ tính bằng giây, đến đúng trạm thu phí thì xe dừng hẳn. Sau khi trả phí, xe ô tô bắt đầu chuyển động nhanh dần đều với vận tốc $v_2(t)=5t(m/s)$, đi được 4 giây, ô tô gặp chướng ngại vật nên phải phanh gấp lần hai.
a) Thời gian từ lúc ô tô phanh lần một cho đến khi dừng hẳn ở trạm thu phí là 3 giây.
A. Đúng
B. Sai
b) Quãng đường ô tô đi được từ lúc đạp phanh đến khi dừng ở trạm thu phí là $36,75 m$.
A. Đúng
B. Sai
c) Vận tốc của ô tô tại thời điểm người tài xế phanh gấp lần hai là $20(m/s)$.
A. Đúng
B. Sai
d) Tổng quãng đường ô tô chuyển động từ lúc phanh lần một đến lúc phanh lần hai là $76,75 m$.
A. Đúng
B. Sai
Câu 2. Một tháp trung tâm kiểm soát không lưu ở sân bay có độ cao $100m$. Trên đỉnh tháp đặt một Ra đa có phạm vi theo dõi $500km$. Chọn hệ trục tọa độ $Oxyz$ có gốc $O$ trùng với vị trí chân tháp, mặt phẳng $(Oxy)$ trùng với mặt đất sao cho trục $Ox$ hướng về phía tây, trục $Oy$ hướng về phía nam, trục $Oz$ hướng thẳng đứng lên phía trên (đơn vị trên mỗi trục tính theo kilômét). Một máy bay tại vị trí $A$ cách mặt đất $12km$, cách $350km$ về phía đông và $200km$ về phía nam so với tháp trung tâm kiểm soát không lưu.
a) Rađa ở vị trí có tọa độ $(0;0;0)$.
A. Đúng
B. Sai
b) Vị trí $A$ có tọa độ $(350;200;12)$.
A. Đúng
B. Sai
c) Khoảng cách từ máy bay đến rađa khoảng $403,29km$ (kết quả làm tròn đến hàng phần trăm).
A. Đúng
B. Sai
d) Nếu máy bay giữ nguyên độ cao, tiếp tục bay về phía nam $100km$ nữa thì rađa của trung tâm kiểm soát không lưu không phát hiện được vị trí của máy bay.
A. Đúng
B. Sai
Câu 3. Trong một hộp đựng 5 quả cầu chứa phiếu có thưởng và 10 quả cầu chứa phiếu không có thưởng (các quả cầu cùng hình dạng, kích thước và khối lượng). Hai bạn Bình, An lần lượt lấy ngẫu nhiên (không hoàn lại) mỗi bạn một quả. Bạn Bình lấy trước, bạn An lấy sau.
a) Xác suất bạn Bình lấy được quả cầu chứa phiếu có thưởng là $\frac{1}{2}$.
A. Đúng
B. Sai
b) Biết bạn Bình đã lấy được quả cầu chứa phiếu có thưởng, xác suất để bạn An lấy được quả cầu chứa phiếu có thưởng là $\frac{2}{7}$.
A. Đúng
B. Sai
Câu 4. Cho hàm số $y=f(x)$ có đạo hàm trên $\mathbb{R}\setminus\{1\}$ và đồ thị như hình vẽ bên dưới.
a) Hàm số nghịch biến trên khoảng $(-\infty;-1)$.
A. Đúng
B. Sai
b) Hàm số đạt cực tiểu tại điểm $x_0=3$.
A. Đúng
B. Sai
c) Tiệm cận đứng của đồ thị hàm số có phương trình là $x=0$.
A. Đúng
B. Sai
d) Tâm đối xứng của đồ thị hàm số $y=f(x)$ nằm trên đường tròn tâm $O$ bán kính $R=\sqrt{2}$.
A. Đúng
B. Sai
PHẦN III. Thí sinh trả lời từ câu 1 đến câu 6.
Câu 1. Lượng calo từ tinh bột khuyến nghị hàng ngày cho một người bình thường khoảng 480 đến 1200 calo. Để nạp đủ chất thì người ta cần nạp cả hai loại tinh bột hấp thu nhanh và tinh bột hấp thu chậm vào cơ thể. Biết rằng trong 100g gạo (chứa tinh bột hấp thu nhanh) có khoảng 150 calo và 100g yến mạch (chứa tinh bột hấp thu chậm) có khoảng 50 calo. Hôm nay bạn An đã ăn ít nhất là 200g gạo. Hỏi bạn ấy cần ăn nhiều nhất bao nhiêu gam yến mạch để có thể nạp vào cơ thể lượng calo tối thiểu cần thiết.
Câu 2. Cho hình chóp đều $S.ABCD$ có cạnh đáy bằng $2a$, cạnh bên bằng $3a$. Khoảng cách từ tâm $O$ của mặt đáy đến một mặt bên của hình chóp bằng $a\sqrt{\frac{b}{c}}$, với phân số $\frac{b}{c}$ tối giản và $b>0, c>0$. Tính $T=3c+2b$.
Câu 3. Một biển quảng cáo có dạng hình vuông $ABCD$ cạnh bằng $4m$ và $I$ là trung điểm của đoạn thẳng $CD$. Trên tấm biển đó có đường parabol đỉnh $I$ đi qua $A, B$ và cắt đường chéo $BD$ tại $M$ (tham khảo hình vẽ).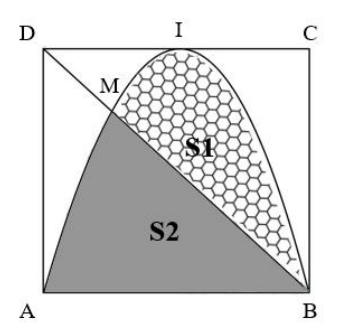
Chi phí sơn phần tô hình tổ ong (có diện tích $S_1$) là $200\,000$ đồng/$m^2$, chi phí sơn phần tô đậm (có diện tích $S_2$) là $150\,000$ đồng/$m^2$ và phần còn lại là $120\,000$ đồng/$m^2$. Số tiền cần chi trả để sơn tấm biển quảng cáo là bao nhiêu nghìn đồng?
Câu 4. Trong không gian $Oxyz$, cho đường thẳng $(d): \frac{x-1}{1} = \frac{y}{2} = \frac{z+2}{1}$ và mặt phẳng $(P): 3x – y + z – 25 = 0$. Một đường thẳng $(d’)$ cắt trục $Oz$ tại điểm $M$, cắt đường thẳng $(d)$ tại điểm $N$ và $(d’)$ song song với mặt phẳng $(P)$. Độ dài nhỏ nhất của đoạn thẳng $MN$ bằng bao nhiêu? *(Kết quả làm tròn đến hàng phần trăm).
Câu 5. Trong một trường THPT X có tỉ lệ học sinh nữ là 48%. Tỉ lệ học sinh nữ và học sinh nam tham gia tư vấn tuyển sinh do Báo Thanh niên phối hợp với Sở GDĐT tổ chức lần lượt là 18% và 15%. Gặp ngẫu nhiên một học sinh của trường. Biết rằng học sinh đó có tham gia tư vấn tuyển sinh. Tính xác suất học sinh đó là nam (Kết quả làm tròn đến hàng phần trăm).
Câu 6. Một doanh nghiệp dự định sản xuất 200 máy tính bảng dành cho học sinh. Nếu doanh nghiệp đó bán $x$ máy tính bảng ($1 \le x \le 200, x \in \mathbb{N}$) thì giá bán cho mỗi máy tính bảng là $p(x) = 4000 – 10x$ (nghìn đồng), trong đó chi phí để sản xuất mỗi máy tính bảng là $c(x) = x^2 – 70x + 400 + \frac{1000}{x}$ (nghìn đồng). Hỏi doanh nghiệp đó sẽ bán bao nhiêu máy tính bảng để lợi nhuận cao nhất?


